Time domain 과 Frequency domain의 이해(1/8)

Health&Program 2021. 5. 7. 20:44

2021. 5. 7. 20:44

Time domain

시간에 따라 변하거나 불변하거나 하는 데이터를 다루는 차원을 의미합니다.

예시를 들어 보자면

- 초 단위로 움직이는 시계의 초침의 회전 각도, 또는 시계 원점 기준으로 변하는 초침 끝의 X, Y 좌표

- 설정 fps 마다 다른 단위의 시간으로 바뀌는 영상

- 음악을 들을 때 박자 단위로 바뀌는 음

일상생활에 흔하게 볼 수 있는 것들입니다.

위의 예시 중 시계 예시를 들어 보겠습니다.

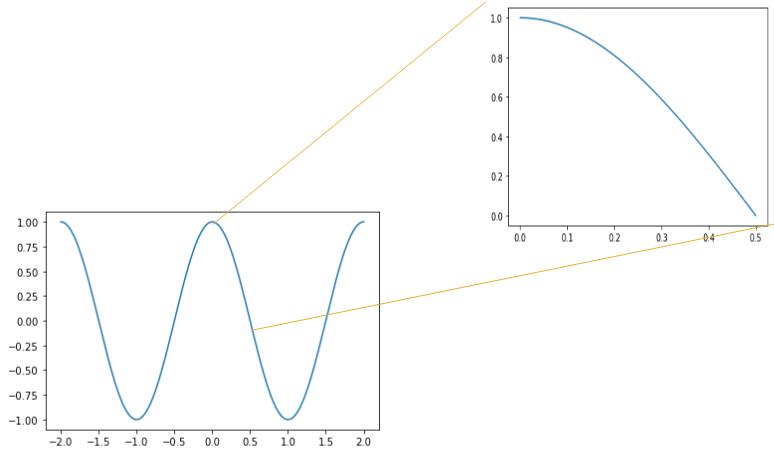
시계를 이용한 Time domain 예시 1

X축 : 초 단위

Y축 : 초침 끝 X축의 위치

측정 시작 시각 : 00시 00분 00초

시계의 반지름 : 5(단위 생략)

코드 구현을 어느 정도 해보신 분들은 다시 겠지만 X 축이라 cos 그래프를 예상했을 수도 있습니다.

설명에서 시계는 00시 00분 00초 즉 90도부터 시작하기 때문에 phase shift로 인해 sin 그래프로 보입니다.

import math 
import matplotlib.pyplot as plt
import numpy as np
#반지름이 5인 시계
watchsize = 5

#초침의 시작점은 00시00분00초 시작점
#degree는 90도
startRadian = math.pi / 2 

x = np.linspace(-2, 0, 2000)
time = np.linspace(60, 0, 2000)
y = []

for addRadian in x:
    y.append(watchsize * math.cos((math.pi * addRadian) + startRadian))

plt.xlabel('second')
plt.ylabel('second hand x location')
plt.plot(time,y, )

위의 코드를 실행시키려면 아나콘다 환경에서 numpy, matplotlib를 설치해야 확인할 수 있습니다.

Time domain으로 데이터를 표현하면 이처럼 시간에 따라 변하는 데이터를 좀 더 직관적으로 표현할 수 있습니다.

하지만 이런 Time domain의 데이터를 모두 담기에는 너무 많은 용량이 필요하게 될 것입니다. 왜냐하면 시간은 흐르고(X축 증가), 시계는 고장 나지 않는 이상 초침의 X축 위치는 계속 변하기(Y축 변동) 때문입니다. 그리고 Time domain에서의 상세한 분석은 어느정도 한계가 있습니다. 이 부분은 무선 통신 분야로 설명하겠습니다.

무선채널에서의 신호를 이용한 Time domain 예시 2

무선 채널 환경에서는 노이즈가 존재합니다. 이 노이즈가 섞인 수신 데이터들은 Time domain으로 해석한다면 원하는 신호와는 거이 다른 신호가 되어있겠죠.

Band-Pass filter는 실제 무선채널 환경에 내보내기 전에 신호에 적용하는 필터입니다. 현 포스팅에서는 다루지 않겠습니다. 위의 신호를 수신단에서 수신하면 어떻게 되어 있을까요?

import math 
import matplotlib.pyplot as plt
import numpy as np
import random 

#-0.5~0.5 사이의 랜덤 값 추출
def makeNoise():
    if (random.random()>0.5):
        return random.random() / 2
    else:
        return -random.random() / 2

#증폭 1
amplitude = 1

#위상차이 0
phaseshift =0


x = np.linspace(0, 0.5, 200)
y = []

for addRadian in x:
    y.append((amplitude * math.cos((math.pi * addRadian) + phaseshift)) + makeNoise())
    #y.append((amplitude * math.cos((math.pi * addRadian) + phaseshift)))

plt.plot(x,y)

노이즈 채널은 상용하고 있는 채널 모델은 아닙니다. 간단하게 -0.5~0.5 사이의 값만 랜덤으로 적용시킨 것입니다.

채널 모델 부분도 현 포스팅에서는 다루지 않겠습니다.

이처럼 노이즈 포함된 신호가 되어있을 것 입니다. 이럴 경우 Time domain으로의 수신 신호 분석은 힘들어질 것 입니다.

하지만 이 신호를 Frequency domain으로 분석한다면 좀 더 해석하기 용이하게 변합니다.

Time domain의 설명은 여기까지 입니다. 몇 가지 내용이 더 있지만, 이번 포스팅의 목표는 Time domain과 Frequency domain을 duality 측면에서 인사이트를 얻는 것 이기 때문입니다.

헬스쟁이 프로그래머