목표
- MSE Loss, MAE Loss, Huber Loss 함수를 이해한다.
- 강화학습 관점에서 각 Loss 함수의 장단점을 이해한다.
MSE(Mean Square Error) Loss 함수
- 평균 제곱 오차를 의미한다.
- 아래 그림은 강화학습에서 MSE를 적용했을때 TD error 값을 어떻게 처리했는지 알 수 있다.
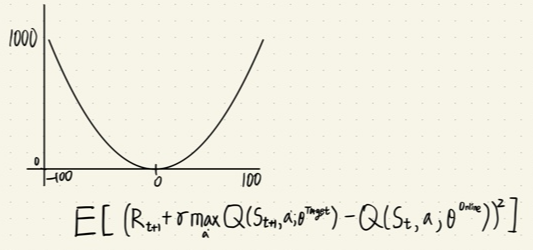
- MSE Loss 함수 장점
- Loss 값이 0에 가까울 수록 경사가 줄어드면서 backpropagation 시 이동시키는 거리가 작아짐으로 수렴을 도와준다.(최적화에 용이)
- 강화학습에서 MSE Loss 함수의 단점
- TD error 값의 절대값이 클 수록 Loss 값이 기하급수적으로 커진다. -> 모든 TD error 범위의 값에 대해서 평등한 Loss 계산이 안된다는 뜻이다. (모든 error에 대한 평등한 Loss 값 x)
MAE(Mean Absolute Error) Loss 함수
- 평균 절대값 오차를 의미한다.
- 아래 그림은 강화학습에서 MAE를 적용했을때 TD error 값을 어떻게 처리했는지 알 수 있다.

- MAE Loss 함수 장점
- 모든 error 값에 대해서 평등한 Loss 값 제공. (모든 error 값에 대해 공평함)
- 지도학습에서 MAE Loss 함수의 단점
- backpropagation시 수렴이 힘듬 (최적화가 힘듬)
Huber Loss 함수
- MSE Loss 함수의 장점과 MAE Loss 함수의 장점을 섞었다.
- 최적화에 용이 + 모든 error 값에 대해서 공평

- delta 라는 임계값을 두고 error 값을 delta 값과 비교하여 MSE Loss 함수와 MAE Loss 함수를 조건에 따라 쓰는 방법이다.
- delta 값이 0 이면 MAE Loss 함수만 쓰고, delta 값이 무한대이면 MSE Loss 함수만 쓰게 된다.
- 보통 delta 값은 1로 두고 사용한다.
정리
- 강화학습에서는 Huber Loss가 좋고 delta 값을 1로 두고 사용한다.
- MSE Loss 함수는 모든 error 값에 대해 공평하지 않다.
- MAE Loss 함수는 최적화 기법에 사용하기에는 힘들다.
- Huber Loss 함수는 delta 임계값을 두고 MSE Loss 함수와 MAE Loss 함수를 조건에 따라 바꿔가며 사용한다.
- Pytorch 모듈에는 이미 Huber Loss 함수가 구현되어 있다. [LINK]
'M.S > Reinforcement learning' 카테고리의 다른 글
| Policy Gradient 수학적으로 풀어보기 (0) | 2025.05.05 |
|---|---|
| 가치 기반 심층 강화학습의 Sample Efficiency를 향상 시킨 Dueling DQN, PER (0) | 2022.08.20 |
| DDQN(Double Deep Q Network) - DQN의 overestimation 극복 (0) | 2022.08.12 |
| Deep Q Network(DQN)-가치 기반 심층 강화학습의 기초 (0) | 2022.08.11 |
| NFQ (Neural Fitted Q-Iteration)를 이용한 Q - function 근사화 (0) | 2022.08.09 |