목표
- 기존의 tabular 기반 MC, TD 방법의 한계점을 이해한다.
- Deep Neural Network를 이용한 Q - function근사화 방법을 이해하고 구현한다. (2 종류의 DNN)
- 기존의 TD 방법을 DNN의 학습 방법으로 매칭 시키며 이해하고 설명 가능해야 한다.
기존 MC-control, TD(Q-learning, SARSA) control의 한계점
- 기존의 MC-control, TD control은 table 형태로 저장하여 Value function 또는 Action value function을 업데이트하고 저장했다.
- 하지만 이 방법의 근본적인 문제는 table 형태로 모든 state에 대해서 각 Value function과 Action value function을 저장하고 있어야 한다는 문제점이 있었다.
- 따라서 State가 연속적인 값이거나 많은 State로 구성된 Environment인 경우에는 비현실적으로 매우 많은 state를 기억하고 있어야 하는 문제가 있었다.
Deep neural network의 도입

- 지도 학습에서 많이 쓰이는 Neural network 구조이다.
- 기존의 perceptron 메커니즘을 조합하여 구성한다.

- 이번에 소개하는 NFQ는 2가지 타입의 DNN 구조를 이용하여 Q-function approximation을 한다.
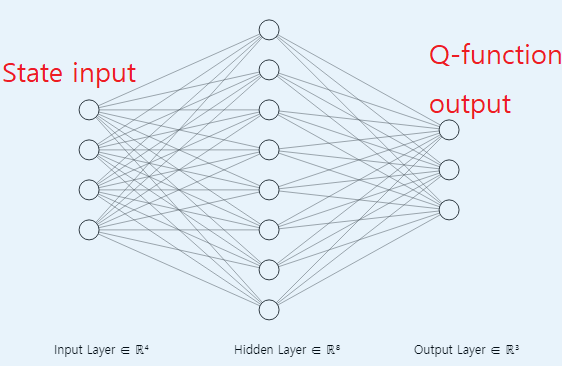
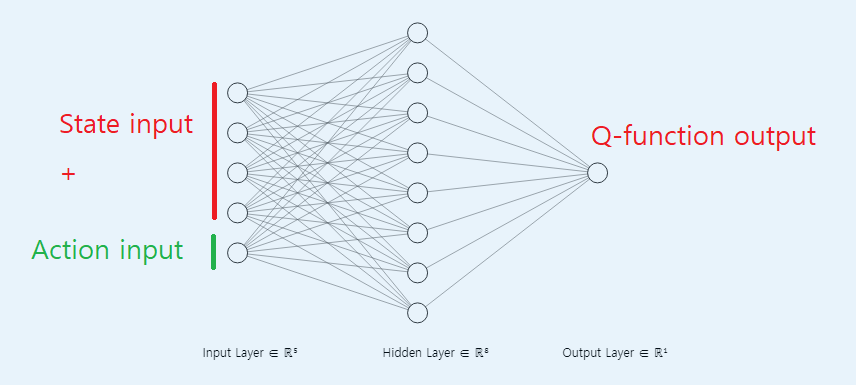
- 두 타입 모두 추 후 사용하게 될 구조임으로 강화 학습에 DNN을 어떻게 적용했는지 숙지해야 한다.
- DNN Class 정의 코드 (pytorch 이용)
class FCQ(nn.Module):
def __init__(self,
input_dim,
output_dim,
hidden_dims=(32,32),
activate_fc=F.relu):
super(FCQ,self).__init__()
# 활성화 함수 설정 (보통 ReLu 사용)
self.activation_fc = activate_fc
# 입력 레이어 정의
self.input_layer = nn.Linear(input_dim, hidden_dims[0])
# 은닉 레이어 설정 (여러 Layer 등록을 위해 List로 정의)
self.hidden_layer =nn.ModuleList()
# 반복문을 이용하여 여러 Layer를 등록함.
for i in range(len(hidden_dims) - 1):
hidden_layer=nn.Linear(hidden_dims[i], hidden_dims[i+1])
self.hidden_layer.append(hidden_layer)
# 출력 레이어 정의
self.output_layer = nn.Linear(hidden_dims[-1], output_dim)
# 모델에 입력시 사용할 함수
def forward(self, state):
# state 입력
x = state
# state 값이 torch.Tensor 타입이 아닐 경우 변환
if not ininstance(x, torch.Tensor):
x = torch.Tensor(x, device=self.device, dtype=torch.float32)
x = x.unsqeeze(0)
# 입력레이어 통과후 활성화 함수 적용
x = self.activation_fc(self.input_layer(x))
# 은닉레이어 통과후 활성화 함수 적용 반복
for hidden_layer in self.hidden_layers:
x = self.activate_fc(hidden_layer(x))
# 출력레이어 통과
x = self.output_layer(x)
# 결과값 출력
return x- 다음은 Loss 함수에 대한 설명이다. 간단하게 MSE(mean squared error)를 사용한다.
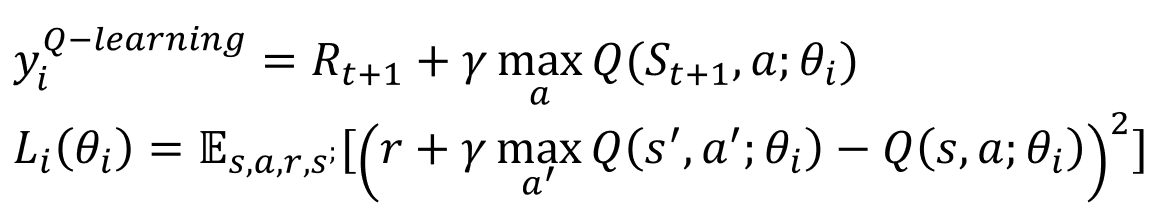
# 다음 state의 Q function을 모두 가져옴
q_sp = self.online_model(next_states).detach()
# 다음 state의 Q function들 중 최대값을 가져옴
max_a_q_sp = q_sp.max(1)[0].unsqeeze(1)
# Q function target을 계산함.
target_q_s = rewards + self.gamma * max_a_q_sp * (1 - is_terminals)
# 현재 state의 Q function 값을 가져옴. 이때 모델은 입실론 그리디 정책으로 행동을 선택을 기준으로함.
q_sa = self.online_model(state).gather(1, actions)
# E [ (Q function target - Q function) ^ 2 ]
MSELoss(target_q_s, q_sa)- 입실론 그리디 정책을 기반으로 학습시킨다.
class EGreedyStraregy():
...
def select_action(self, model, state):
self.exploratory_action_take = False
with torch.no_grad():
q_values = model(state).cpu().detach().data.numpy().squeeze()
if np.random.rand() > self.epsilon:
action = np.argmax(q_values)
else:
action = np.random.randint(len(q_values))
return action- Optimizer 함수는 Adam, RMSProp 등이 있다.
- 주로 미니 배치 단위로 S, A, R, S'을 모으고 배치 단위로 학습시킨다.
정리
NFQ의 한계점(중요)
- 동일한 DNN을 이용하여 학습을 시킨다. 즉 현재 state, action 값에 대해서 학습을 하면서 다른 state, action값의 바뀐다.
미니 배치 단위로 학습을 하면서 target으로 하는 state, action 짝만 학습시키려고 함으로써 다른 비슷한 state, action 값이 안정적으로 수렴하지 힘들다.
- IID(independent and identically distribution) 가정을 지키기 못한다. 미니 배치 단위로 모델을 학습시킨다. 하지만 미니배치 학습을 주기로 매번 Q-function 값이 달라지게된다. 이는 매 주기마다 수집하는 미니배치 샘플들이 서로 다른 분포에서 샘플링된다는 뜻이다.
- 미니배치 데이터들이 시간 관계성이 있다. DNN 모델을 시간 관계가 있는 데이터를 기반으로 학습 시킨다면 오버피팅 된다. (Q-function approximation 기능을 RNN이나 LSTM으로 대체 한다면 괜찮을 지도..?)
'M.S > Reinforcement learning' 카테고리의 다른 글
| DDQN(Double Deep Q Network) - DQN의 overestimation 극복 (0) | 2022.08.12 |
|---|---|
| Deep Q Network(DQN)-가치 기반 심층 강화학습의 기초 (0) | 2022.08.11 |
| 강화학습 Agent를 이용한 MC control, SARSA, Q-Learning (0) | 2022.08.05 |
| Model free 환경에서 사용하는 MC와 TD를 이용한 Value function prediction (0) | 2022.07.25 |
| Multi Armed Bandit(MAB) (0) | 2022.07.21 |