Model free 환경
- MDP 가 주어져 있지 않은 상태를 의미한다.
-> 모든 정보가 수학적으로 기술되어 있지 않음.
- State transition matrix, 모든 State, Reward를 모르는 상황이다.
-> Agent가 직접 탐색을 해야하는 상황임.
- 내가 관심있는 강화 학습은 Model free 환경이다.
-> 현실 세계는 Model free라 생각한다. 현실은 매우 다양한 환경요소 때문에 확률적으로 매우 분산이 큼.
- Model free 환경에서 현재 policy에 따르는 Value Function을 평가해야 한다.
-> Value Function을 구하면 현재 policy를 따랐을 때 얻을 수 있는 expected return 값을 매 state 마다 구할 수 있다.
Model free 환경에서 policy를 평가하는 2가지 방법
Monte Carlo prediction(MC)
- First-visit MC
1. Value function은 현재 state부터 termianl state까지의 감가율을 적용한 expected return 값이다.
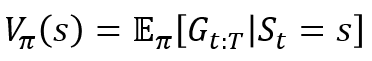

2. MC 방법을 통해 무한대에 가까운 시뮬레이션을 할 경우 Value function 값은 현재 policy의 value function에 수렴한다. (하지만 수렴이 힘들고 분산이 클 것임 -> state, action, reward, next state로 구성된 tuple 집단이 유사한 trajectory를 구하는 것은 힘들다는 뜻)



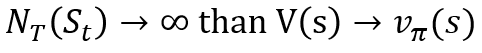
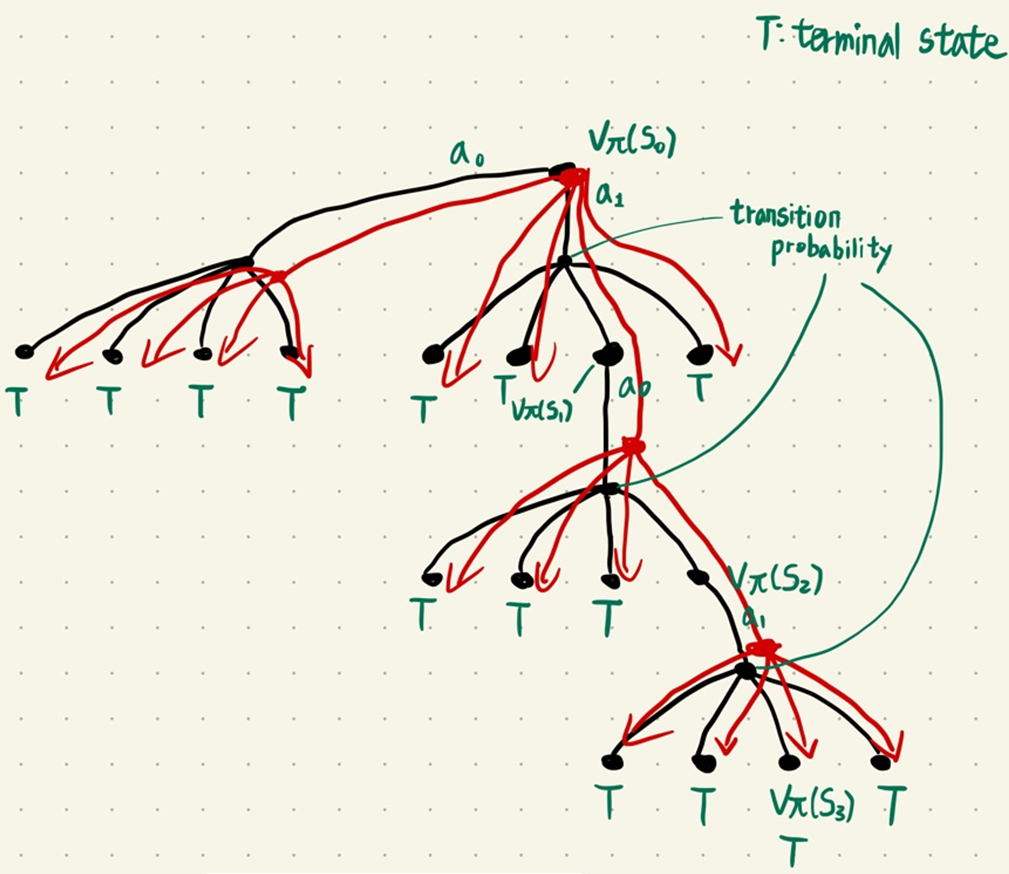
3. 좀 더 효율적으로 계산하기 (모든 trajectory를 기억하지 않고, episode가 끝날 때마다 update 하기)

4. 독립적이면서 동일한 분포(independent and identically distributed, IID)에서 trajectory를 형성함으로써 무한개의 tracjtory value-function이 수렴하는 것을 확인 가능.
- Every-visit MC
1. First-visit MC를 공부하다보면 1개의 trajectory에서 2번 이상 같은 state에 방문한다면 어떻게 해야할까? First-visit MC 방법을 고집할까? 아니면 다시 계산할까?
2. 이런 문제를 다루기 위해 Every-visit MC가 있다.
3. IID 는 아니지만 수렴함을 확인함.

4. trajectory 생성 함수
def generate_trajectory(pi, env, max_steps=200):
done, trajectory = False, []
while not done:
state = env.reset()
for t in range(max_steps)
action = pi(state)
next_state, reward, done, _ = env.step(action)
experience = (state, action, reward, next_state, done)
trajectory.append(experience)
if done:
break
state = next_state
return np.array(trajectory)5. MC prediction 함수
def mc_prediction(pi,
env,
gamma=1.0,
init_alpha=0.5,
min_alpha=0.01,
alpha_decay_ratio=0.5,
n_episodes=500,
max_steps=200,
first_visit=True):
#모든 state의 갯수를 가져옴
nS = env.observation_space.n
#감가 계수 미리 계산 0.99 ~ 0.3695
discounts = np.logspace(0, max_steps, num=max_steps, base=gamma, endpoint=False)
#decay하는 alpha 값도 미리 계산
alpha = decay_schedule(init_alpha, min_alpha, alpha_decay_ratio, n_episodes)
#value-function 초기화
V = np.zeros(nS, dtype=np.float64)
#episode 별 value-function을 보기위함.
V_track = np.zeros((n_episodes, nS), dtype=np.float64)
#dictionary로 state 별 value function을 저장함.
targets = {state:[] for state in range(nS)}
for e in tqdm(range(n_episodes), leave=False):
#1개의 trajectory 생성
trajectory = generate_trajectory(pi, env, max_steps)
#방문 여부 판단용 변수
visited = np.zeros(nS, dtype=np.bool)
#1개의 trajectory 순회
for t, (state, _, reward, _, _) in enumerate(trajectory):
#현재 state 방문 여부 & first_visit 모드인 경우 continue
if visited[state] and first_visit:
continue
#현재 state는 첫 방문이거나, every_visit 모드 인 경우 수행
visited[state] = True
#현재 상태부터 종료 상태까지 step 갯수를 샘
n_steps = len(trajectory[t:])
#Discount를 적용한 return 값을 계산함.
G = np.sum(discounts[:n_steps] * trajectory[t:, 2])
#targets 자료구조에 Discount를 적용한 return 값 저장
targets[state].append(G)
#mc error 계산 (현재 tracjtory에서 나온 value function - 기존의 value function)
mc_error = G - V[state]
#alpha 감가율을 적용하여 mc_error 적용
V[state] = V[state] + alphas[e] * mc_error
#trajectory 별 value function의 변화를 확인하기 위해 저장
V_track[e] = V
#최종 Value function, trajectory 별 value function, state 별 추론한 모든 기대값 반환
return V.copy(), V_track, targets6. MC prediction의 단점은 에피소드가 끝날 때까지 기다려야함. (그렇다면 무한 에피소드인 경우??)
7. 장점은 bias에 강함
Temporal-Difference (TD)
1. 단일 step 에서 얻은 Reward 만을 이용하여 Value-function을 추론한다.
2. MC는 에피소드가 끝날때까지 기다려야 하지만 TD는 즉각적으로 계산한다.(bootstrapping)
- bootstrapping
현재의 값을 이용해 미래의 값을 추정하는 방법.
3. TD의 Value-function 구하기 공식

4. Value-function이 현재 state로 부터 기대할 수 있는 return 값이라 하는 것은 변함없고 다음 step의 reward와 감가율을 적용한 공식을 재귀적으로 문제를 해결하였다.
5. TD target과 TD error


- TD target 은 현재 Value-function이 근사 해야하는 값이다.
- TD error 는 현재 Value-function과 TD target의 오차를 의미한다.
def td(pi,
env,
gamma=1.0,
init_alpha=0.01,
min_alpha=0.01,
alpha_decay_ratio=0.5,
n_episodes=500):
#state space 취득
nS = env.observation_space.n
#Value funcion 초기화
V = np.zeros(nS, dtype=np.float64)
V_track = np.zeros((n_episodes, nS), dtype=np.float64)
#TD target 초기화
targets = {state:[] for state in range(nS)}
#감소하는 alpha값 미리 계산
alphas = decay_schedule(init_alpha, min_alpha, alpha_decay_ratio, n_episodes)
for e in tqdm(range(n_episodes), leave=False):
state, done = env.reset(), False
while not done:
#현재 state을 policy에 따라 action
action = pi(state)
#다음 state, reward, done 여부 취득
next_state, reward, done, _ = env.step(action)
#td target 계산
td_target = reward + gamma * V[next_state] * (not done)
#state에 따르는 td_target 저장
targets[state].append(td_target)
#td_error 계산
td_error = td_target - V[state]
#td_error에 alpha 값 적용후 value-function 없데이트
V[state] = V[state] + alphas[e] * td_error
#다음 state로 update
state = next_state
#V-function의 변화 양상 저장
V_track[e] = V
return V, V_track
- n-step TD
- MC 방법과 TD 방법은 서로 극단적인 성향을 가지고있다.
- MC는 episode가 끝나야하고, TD는 1단계의 step만 수행하고 가치를 평가한다.
- 결과적으로 MC는 low bias, high variance, TD는 high bias, low variance 하게 가치를 평가한다. (무한한 샘플링이 가능하다면 둘다 결국 수렴함.)
- MC와 TD 사이의 방법중 하나로 n-step TD가 있다.

간단하게 현재 state의 value function 값을 2개 step 이상의 discount factor가 적용된 reward로 적용하는 것이다.
def n_step_td(
pi,
env,
gamma=1.0,
init_alpha=0.5,
min_alpha=0.01,
alpha_decay_ratio=0.5,
n_step=3,
n_episodes=500):
#state 공간
nS = env.observation_space.n
#Value function 초기화
V = np.zeros(nS, dtype=np.float64)
#episode 별 value function 히스토리 저장
V_track = np.zeros((n_episodes, nS), dtype=np.float64)
#에피소드별 감소하는 alpha 값 미리 계산
alphas = decay_schedule(init_alpha, min_alpha, alpha_decay_ratio, n_epsidoes)
#Discount factor 미리 계산
discount = np.logspace(0, n_step + 1, num=n_step + 1, base=gamma, endpoint=False)
for e in tqdm(range(n_episodes), leave=False):
#state, done 여부, n-step 저장을 위한 path 초기화
state, done, path = env.reset(), False, []
#episode가 끝날때까지 실행
while not done or path is not None:
path = path[1:]
#n-step만큼 step 할때까지 반복 실행
while not done and len(path) < n_step:
action = pi(state)
next_state, reward, done, _ = env.step(action)
experience = (state, reward, next_state, done)
path.append(experience)
state = next_state
if done:
break
# 현재 path에 저장한 경험의 수
n = len(path)
# 평가할 state
est_state = path[0][0]
# path에 저장해왔던 reward만 추출
rewards = np.array(path)[:,1]
# 모든 reward에 discount factor 적용
partial_return = discount[:n] * rewards
# 다음 state의 value function값
bs_val = discounts[-1] * V[next_state] * (not done)
# td target 구하기, discount factor를 적용한 reward에 다음 state의 value function 합하기
ntd_target = np.sum(np.append(partial_return, bs_val))
# td error 구하기
ntd_error = ntd_target - V[est_state]
# td error에 현재 episode에 맞는 alpha 값 적용 후 저장
V[est_state] = V[est_state] + alphas[e] * ntd_error
if len(path) == 1 and path[0][3] == True:
path = None
V_track[e] = V
return V, V_track
- forward-view TD(λ)
- MC 방법과 TD 방법을 섞은 방법이다.
- λ 값을 0 보다 크고 1 보다 작은 사이의 값을 두면 MC 방법과 TD 방법을 동시에 가중치를 두고 쓰는 방법이다.
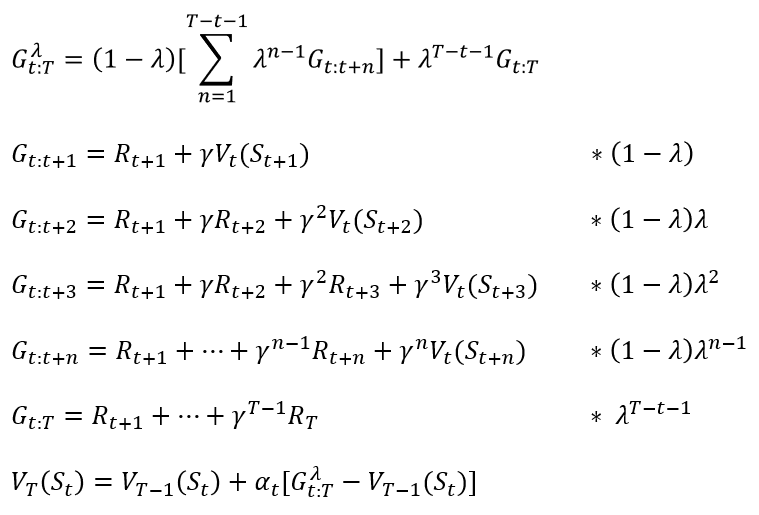
- λ 값이 0 이면 MC의 방법을, 1 이면 TD의 방법을 사용하는 것이다.
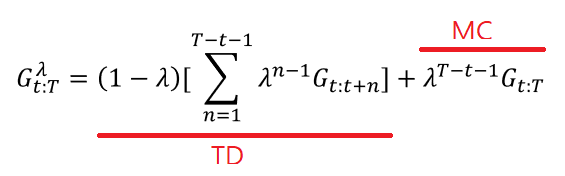
- 하지만 이 방법은 MC 방법과 동일한 문제점인 value function을 추정하는데 있어서 에피소드가 끝날때까지 기다려야하는 문제가 있다.
- backward-view TD(λ)
- forward-view TD 와 달리 eligibility trace 를 이용하여 MC와 TD의 개념을 섞어서 사용함

def td_lambda(
pi,
env,
gamma=1.0,
init_alpha=0.5,
min_alpha=0.01,
alpha_decay_ratio=0.5,
lambda=0.3,
n_epsidoes=500)
# 모든 state 취득
nS = env.observation_space.n
# Value function 초기화
V = np.zeros(nS, dtype=np.float64)
# episode 별 변하는 Value function 초기화
V_track = np.zeros((n_episodes, nS), dtype=np.float64)
# eligibility trace 배열 초기화
E = np.zeros(nS, dtype=np.float64)
# episode 별 감소하는 alphas 미리 계산
alphas = decay_schedule(init_alpha, min_alpha, alpha_decay_ratio, n_episodes)
for e in tqdm(range(n_episodes), leave=False):
# episode를 재시작 할때마다 eligibility trace를 0으로 초기화
E.fill(0)
# env reset
state, done = env.reset(), False
while not done:
action = pi(state)
next_state, reward, done, _ = env.step(action)
#td target 계산
td_target = reward + gamma * V[next_state] * (not done)
#td error 계산
td_error = td_target - V[state]
#현재 방문한 state에 대해서 eligibility trace 배열에 1을 더함
E[state] += 1
#현재 state에서 계산한 td error와 eligibility trace 배열을 모두 곱하고
#모든 state의 value-function에 적용
V = V + alphas[e] * td_error * E
# eligibility trace 배열 감가
E = gamma * lambda * E
state = next_state
V_track[e] = V
return V, V_track
- state를 재방문하는 횟수가 많을 수록 eligibility trace에서 배열의 값은 증가한다.
- 같은 state에 많이 방문 할 수록 큰 가중치로 업데이트 됨.
정리
- Model free 환경에서 value function을 prediction 하는 방법을 공부했다.
- 구하는 과정에서는 필연적으로 주어진 policy를 사용해서 trajectory를 형성해야 한다.
- 형성한 trajectory를 이용해서 MC 또는 TD 방법을 통해 value function을 prediction 했다.
- MC는 평가 하고자하는 state에서 시작하는 trajectory 를 여러개 형성하여 평균값을 통해 value function을 구했다. (bias 가 적은 대신 variance 가 큼)
- MC는 First visit, every visit 방법으로 나뉘고 두 방법은 모두 결론적으로 value-function이 수렴함을 볼 수 있다.
- TD는 평가 하고자 하는 state에서 바로 다음 state의 value function과 reward 만을 이용해서 value function을 구했다.(bias 가 큰 대신 variance 가 적음)
- TD는 n-step TD, forward-view TD(λ), backward-view TD(λ) 방법이 있는데 이 방법들은 모두 MC 방법의 특징과 TD 방법의 특징을 혼합하여 사용하기 위해서 사용되었다.
'M.S > Reinforcement learning' 카테고리의 다른 글
| DDQN(Double Deep Q Network) - DQN의 overestimation 극복 (0) | 2022.08.12 |
|---|---|
| Deep Q Network(DQN)-가치 기반 심층 강화학습의 기초 (0) | 2022.08.11 |
| NFQ (Neural Fitted Q-Iteration)를 이용한 Q - function 근사화 (0) | 2022.08.09 |
| 강화학습 Agent를 이용한 MC control, SARSA, Q-Learning (0) | 2022.08.05 |
| Multi Armed Bandit(MAB) (0) | 2022.07.21 |