간단 설명
1. 다른 강화학습 기법(Q-learning, Sarsa 등..)과 달리 Next state가 없고 오직 Action, Reward 의 형태를 다룬다.
2. Markov Decision Process(MDP) 환경에서 동작시키는 것이 아니다.
3. MAB는 Exploration을 어떻게 할 것인지에 대해 다양한 방법을 제시했다.
용어 설명
1. Regret

- v_*는 현재 state에서 얻을 수 있는 최대 보상값이다.
- v는 현재 state에서 MAB Agent가 action 함으로써 얻는 보상값이다.
- 현재 상태에서 수행한 action에 대한 평가값이라 생각한다.
2. Total regret
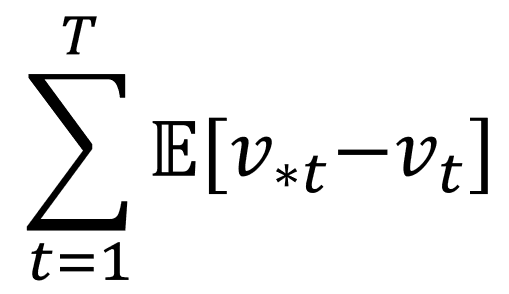
- 왼쪽의 Summation 은 시작지점(Start) t = 1 에서 끝지점(Terminal) T 까지 모두 더한다는 의미이다.
- E[v_*t - v_t]는 t 시점에서 얻었던 Regret 값에 대한 기대값이다. 기대값인 이유는 MAB를 적용할 실제 환경은 확률적이라 가정하기 때문이다.
- 시작지점 -> 끝지점 까지의 Expected Regret값을 Total regret 이라한다. MAB Agent는 이 값을 낮추기 위해서 학습한다.
Total regret을 낮춘다는 것은 Total reward (Return)을 높인다는 것과 같다.
3. Q - function
- MAB 프레임워크에서는 단순하게 action a를 했을때 즉각적으로 얻을 수 있는 expected reward 값이다. expected 가 있는 이유는 확률적인 환경에서 MAB를 구동시키기 때문이다.
Exploration 전략
1. Epsilon-greedy strategy
요약 설명
- epsilon 이라는 Threshold 값을 두고 확률적으로 Random 선택을 하는 방법이다.
- episode가 끝날때 마다 epsilon 값을 지정한 decay_value 만큼 감소 시킨다.
- 많은 episode가 지나면 epsilon 값이 0에 수렴하게 되는데 이때부터는 greedy 하게 선택한다.
내 생각
- 이 방법은 강화학습 프레임워크에서 많이 쓰인다. 최근에 논문을 구현하면서 사용했다.(DQN, SAC, DDPG 등등)
start episode
...
if np.random.uniform() > epsilon:
action = np.argmax(Q)
else:
action = np.random.randint(len(Q))
reward = env.step(action)
N[action] += 1
Q[action] = Q[action] + (reward - Q[action])/N[action]
...
end episode
epsilon -= decay_value2. Optimistic intialization strategy
요약 설명
- Q 값을 높게 잡고 greedy 하게 여러 episode를 거친다. 여기서 높게라는 의미는 기대하는 expected reward 값보다 높게 잡는 것이다.
- 여러 episode를 거치면서 자동으로 Q값들이 낮아지며 결국 모든 action에 대해 expected reward 값을 알게될 것이다.
내 생각
- epsilon-greedy 처럼 if 분기점이 필요없어서 깔끔한 코드가 될 것 같다.
- 단점은 MAB 뿐만아니라 강화학습의 고질적인 문제는 너무 많은 Sampling을 해야한다는 것이다.
Q = np.full(env.action_space.n, optimistic_estimate)
N = np.full(env.action_space.n, initical_count)
...
#only
action = np.argmax(Q)
reward = env.step(action)
N[action] += 1
Q[action] = Q[action] + (reward - Q[action])/N[action]3. Softmax strategy

요약 설명
- B 는 action space 집합이다.
- tao 값은 episode가 끝날때마다 감소한다.
- tao 값이 크면 Softmax 의 확률 분포가 균등하게 나타난다. tao 값이 작으면 Q-function의 값에 따른 확률 분포가 나온다.
- 결국 처음에는 exploration, 후반에는 greedy 하게 선택하는 원리이다.
- 딥러닝 Output fuction 계열에서 확률 분포로 쓰이는 Softmax와 똑같은 원리로 쓰인다.
scaled_Q = Q / tao
norm_Q = scaled_Q - np.max(scaled_Q)
exp_Q = np.exp(norm_Q)
probs = exp_Q / np.sum(exp_Q)
action = np.random.choice(np.arange(len(probs)), size=1, p=probs)[0]
reward = env.step(action)
tao -= decay_unit4. Upper confidence bound(UCB) strategy

요약 설명
- Q값의 추정치가 불확실한 경우 해당 Q 값을 exploration 할 수 있도록 장려하는 방법이다.
- argmax 대괄호 안에 오른쪽 텀을 U_t 라 함.
- U_t 의 e 는 현재까지 모든 action을 한 횟수, N_e(a) 는 현재까지 action a를 수행한 횟수.
- 모든 action 대비 현재 action a를 적게할 경우 U_t 값이 증가한다.
- 같은 action을 많이 할 경우 U_t 텀이 작아진다.
- c는 U_t 텀에 대한 가중치 이다.
U_t = np.sqrt(c * np.log(e)/N)
action = np.argmax(Q + U_t)
reward = env.step(action)5. Thompsom sampling strategy
요약 설명
- Q 값이 가우시안 분포를 따르는 것으로 시작한다. (평균, 표준편차)
- Agent가 계속 action을 수행 할 수록 평균값은 명확해지고 표준편차는 줄어든다.
- alpha, beta 파라미터를 이용한다.
- alpha와 beta는 action space의 사이즈만큼 존재한다.
- alpha는 Q값의 초기 표준편차 값을 의미한다. alpha는 episode를 반복할수록 줄어드는데 beta는 alhpa값이 감소하는 속도를 조절한다.
samples = np.random.normal(loc=Q, scale=alpha/(np.sqrt(N) + beta))
action = np.argmax(samples)
reward = env.step(action)'M.S > Reinforcement learning' 카테고리의 다른 글
| DDQN(Double Deep Q Network) - DQN의 overestimation 극복 (0) | 2022.08.12 |
|---|---|
| Deep Q Network(DQN)-가치 기반 심층 강화학습의 기초 (0) | 2022.08.11 |
| NFQ (Neural Fitted Q-Iteration)를 이용한 Q - function 근사화 (0) | 2022.08.09 |
| 강화학습 Agent를 이용한 MC control, SARSA, Q-Learning (0) | 2022.08.05 |
| Model free 환경에서 사용하는 MC와 TD를 이용한 Value function prediction (0) | 2022.07.25 |